A markov model can be used to examine a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Let’s define a stochastic process that takes on a finite number of possible values which are nonnegative integers. Each state,
, represents it’s value in time period
. If the probability of being in
is dependent on
, it’s refered to as the first-order Markov property. We are interested in estimating
, which is the fixed probability that
at time
will be followed by state
. These
step transition probabilities are calculated through the Chapman-Kolmogorov equations, which relates the joint probability distributions of different sets of coordinates on a stochastic process. Markov chains are generally represented as a state diagram or transition matrix where every row of the matrix,
, is a conditional probability mass function.
Let’s consider an example using website pathing data from an ecommerce website. The set of possible outcomes, or sample space, is defined below. For this example, takes the values of each page on the site. This likely violates the Markov property, given that pages on an ecommerce website aren’t generally dependent on the previous page visited, but let’s proceed anyways.
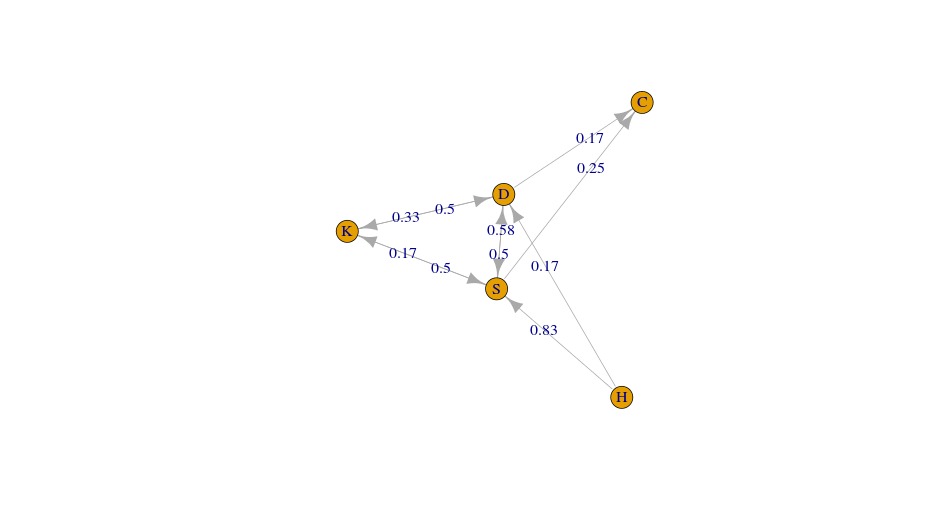
Given a series of clickstreams, a markov chain can be fit in order to predict the next page visited. Below are the state diagram and transition matrix for this data. It suggests that from the home state, there is a 83% probability that a visit to the shoes state will be next.
To be honest, I’m not certain whether is the best technique to model how consumers utilize a website. Markov chains seem to be promising, but I’m a little uneasy about whether our assumptions are met in such scenarios. If you have ideas for such problems, please comment below.